第一课_第三周学习笔记¶
内容概要：
四种常用的激活函数、导数，以及为什么需要非线性激活函数
神经元模型
参数随机初始化，为什么不能将所有参数初始化为0
单隐层神经网络简介
分步骤实现单隐层神经网络（forward propagation & back propagation）
TensorFlow 中实现单隐层神经网络
0 - 符号说明¶
| 符号 | 含义 |
|---|---|
| $X$ | 堆叠（stack）所有输入样本得到的输入矩阵 |
| $x^{(i)}$ | 数据集中的第 $i$ 个样本的输入向量 |
| $Y$ | 堆叠（stack）之后的真实值（标签）向量 |
| $y^{(i)}$ | 第 $i$ 个样本的真实值（标签） |
| $\hat{y}^{(i)}$ | 第 $i$ 个样本的最终预测值 |
| $a^{(i)}$ | 训练过程中，第 $i$ 个样本的预测值 |
| $A$ | 训练过程中，所有样本的预测值矩阵 |
| $m$ | 输入样本数量 |
| $n$ | 每一个样本的特征数量 |
| $w_i$ | 第 $i$ 个特征的权重系数 |
| $W$ | 所有特征的权重系数向量 |
| $b$ | 线性回归中的截断误差 |
| $Z$ | 神经元中的线性计算结果矩阵，激活函数的输入 |
1 - 激活函数¶
激活函数是神经网络中非常关键的一个组成部分，常用的激活函数都是非线性的，如sigmoid、tanh、ReLU、Leaky_ReLU等。四种常用激活函数的图像如下：
为什么要使用非线性激活函数？
如果不使用非线性激活函数，那个神经网络仅仅是将输入线性组合后输出，而两个线性方程的组合依然是线性方程。这样的话，神经网络就没法逼近复杂的非线性函数。当然，在一些比较特殊的问题中，如回归等，也会使用线性激活函数。
1.1 - sigmoid & tanh¶
sigmoid 常用于二分类（binary classification）网络的输出层；在隐藏层中，通常使用 tanh，而不是sigmoid。这主要是因为tanh的输出为（-1，1），均值为0，所以下一层的输入是centered；而sigmoid的均值是0.5。tanh其实就是sigmoid在y轴方向向下移动1个单位的版本。
sigmoid函数表达式及其导数如下：
$$f(x) = \frac{1}{1+e^{-x}}\tag{sigmoid函数}$$$$f(x)^{'} = f(x)(1-f(x))\tag{sigmoid导数}$$tanh函数表达式及其导数如下： $$f(x) = tanh(x)\tag{tanh函数}$$
$$f(x)^{'} = 1-f(x)^{2}\tag{tanh导数}$$1.2 - ReLU & Leaky_ReLU¶
ReLU (Rectified Linear Unit)激活函数在深度学习中比sigmoid和tanh更常用。 当激活函数的输入z的值很大或很小的时候，sigmoid和tanh的梯度非常小，这会大大减缓梯度下降的学习速度。所以与sigmoid和tanh相比，ReLU的训练速度要快很多。Leaky ReLU比ReLU要表现得稍微好一丢丢但是实践中大家往往都用ReLU。
$$f(x) = max(0, x)\tag{ReLU函数}$$2 - 神经元¶
典型的神经元如下图所示：
神经元中包含两个计算过程：
step1. 由线性方程计算输入向量 $x$ 的线性回归值,即 $z=w^Tx+b$ ；
step2. 将线性回归值输入激活函数 $\alpha=\sigma(z)$，得到结果。
可以发现，神经元长得和LR一样。事实上，当神经元采用sigmoid函数作为激活函数时，就是LR模型，因此，LR是神经元的一个特例。
3 - 参数随机初始化¶
和LR模型一样，每一个神经元中都有两组参数，$w$ 和 $b$。
对于Logistic Regression，将参数初始化为0没有问题；但是，在神经网络中，如果将所有参数初始化为0，再使用梯度下降算法训练，就会完全无效。因为，所有参数初始化为0之后，单个隐层中的所有神经元每一次迭代的计算内容就完全一样了，参数更新也一样，也就是说参数矩阵的每一行的元素都是一样的，这样就无法达到训练的目的。
随机初始化参数可以解决以上问题。ng给出的一个初始化方法是使用 np.random.randn(n_h, n_x)*0.01 ,即：使用标准正态分布（又称“高斯分布”）生成均值为0，方差为1的随机数，然后乘以0.01。当 $w$ 初始化为均值为0.01的正态分布随机数之后，参数 $b$ 初始化为0也是可以的。
4 - 单隐层神经网络简介¶
将若干个神经元分层组合，就是神经网络。典型的单隐层神经网络结构如下图：
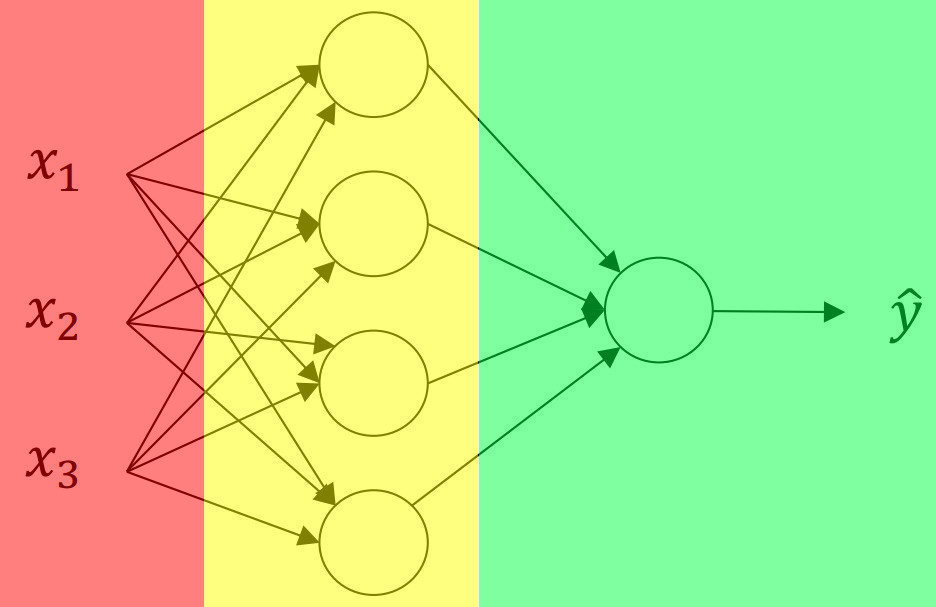其中，红色覆盖的是【输入层】，黄色覆盖的是【隐含层】，绿色覆盖的是【输出层】。
上图中，隐层中有4个神经元，神经元数量可以根据任务的需求调整。
由于输入层没有任何计算，仅仅是数据的输入，在计算神经网络的层数时，通常不考虑输入层。因此，单隐层神经网络的层数是2。
5 - 单隐层神经网络的实现过程¶
单隐层神经网络的实现主要有以下几个步骤：
step 1. 定义网络结构，即：确定输入层、隐含层和输出层的units数量
step 2. 随机初始化网络参数
step 3. 循环迭代训练，更新参数
1. 执行前向传播（forward propagation）
2. 计算损失（loss）
3. 执行后向传播（backward propagation），得到所有参数的梯度（gradients）
4. 使用梯度下降法（gradient descent）更新参数
step 4（可选）. 调参：hidden layer size、learning rate等
Note: 参数更新方法可以视情况调整，在很多问题中，Adam的表现会优于其他方法。
5.2 - 随机初始化参数¶
这一步主要是将 连接输入层与隐含层的 $W_1$ 和 $b_1$ 以及 连接隐含层与输出层的 $W_2$ 和 $b_2$ 随机初始化。通常使用标准正态分布进行随机初始化。在后面的课程中，ng还介绍了一些更为有效的参数随机初始化方法。
切记：不能将所有参数初始化为0！！！
5.3.1 - 执行前向传播（forward propagation）¶
前向传播分为两个步骤：linear forward和activation forward。
对于单个样本 $x^{(i)}$， 其前向传播过程的相关计算如下: $$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}$$ $$a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}$$ $$z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}$$ $$\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}$$ $$y^{(i)}_{prediction} = \begin{cases} 1 & \mbox{if } a^{[2](i)} > 0.5 \\ 0 & \mbox{otherwise } \end{cases}\tag{5}$$
对于全部样本的计算，在Python中实现时采用向量化的计算方法，即将所有输入样本堆叠成一个输入矩阵，然后再分别执行每一层的 linear forward 和 activation forward。
Note：每一层 activation forward 过程中使用的激活函数可以不一样，通常隐含层使用tanh，输出层使用sigmoid。
5.3.2 - 计算损失（loss）¶
得到所有样本的预测值后，使用以下公式计算损失Loss（又称“训练成本 cost”）： $$J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small $$
5.3.3 - 执行后向传播（backward propagation），得到所有参数的梯度（gradients）¶
后向传播过程与前向传播过程的计算路线相反，先计算输出层（第2层）相关参数的梯度，然后计算隐含层（第1层）相关参数的梯度，其计算公式如下图：
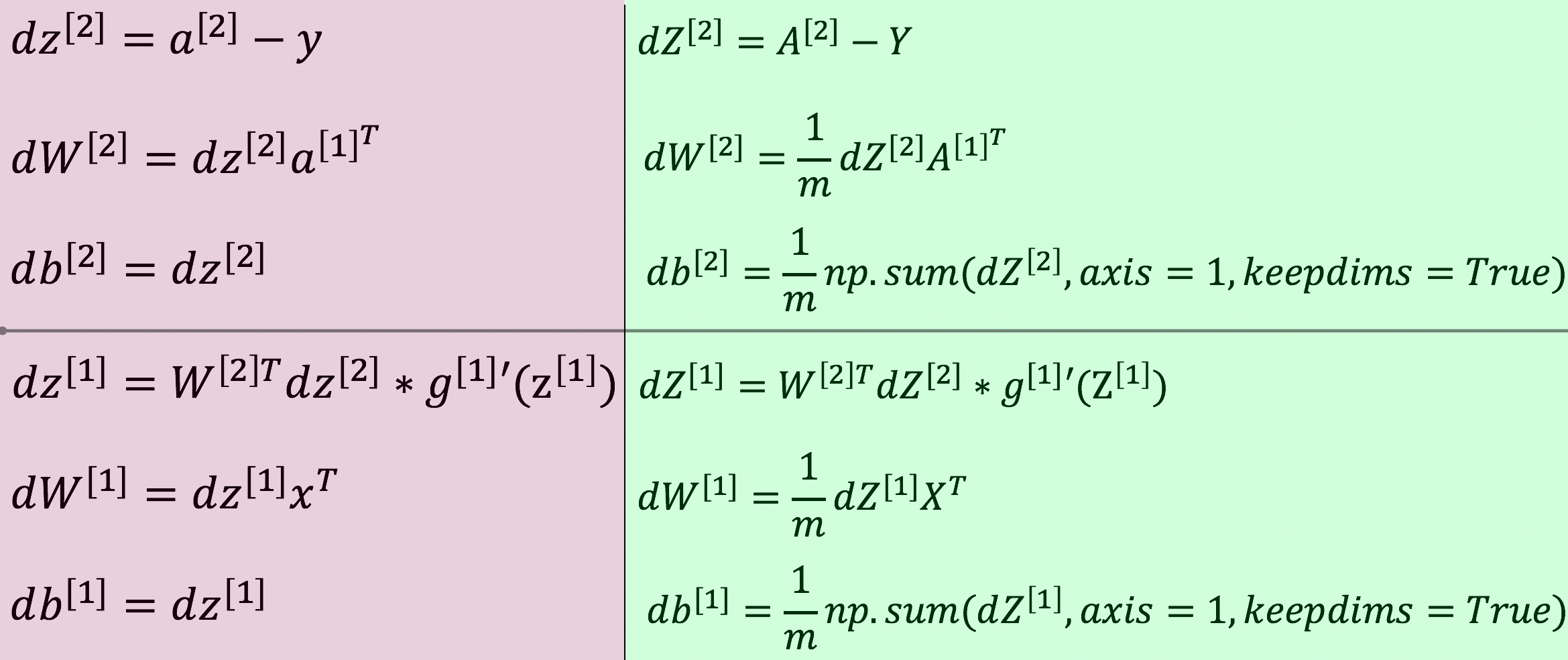图中，棕色色块覆盖的部分表示单个样本的后向传播计算过程；绿色色块覆盖的是所有样本的堆叠在一起之后的后向传播向量化计算过程，也就是python实现后向传播过程所参照的计算公式。
5.3.4 - 使用梯度下降法（gradient descent）更新参数¶
gradient descent参数更新规则: $$ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$$ 其中：$\alpha$ 是学习率（learning rate）；$\theta$ 是需要更新的参数
学习率（learning rate）大小的设定对梯度下降法有着显著的影响，下面有两张动图（Adam Harley制作的）可以展示学习率设定好坏对梯度下降过程的影响：
好的学习率（learning rate）大小，随着训练的进行，逐步逼近函数最小值：
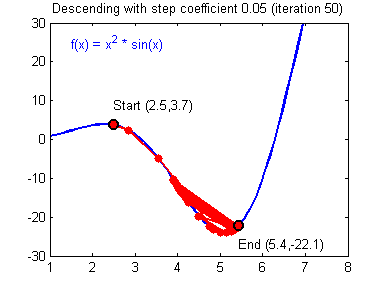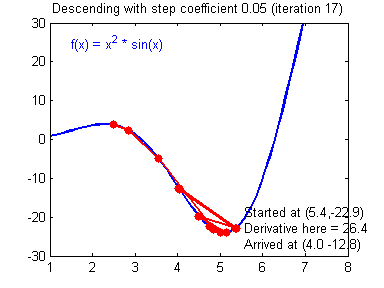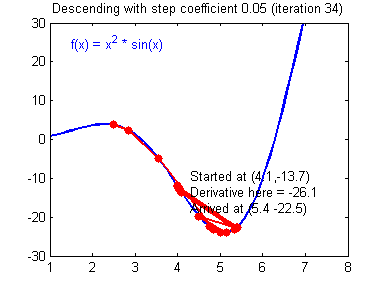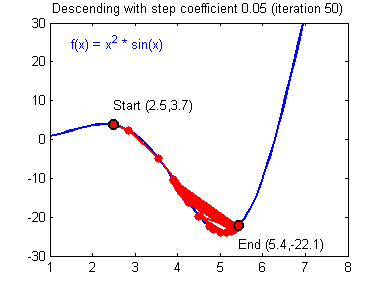
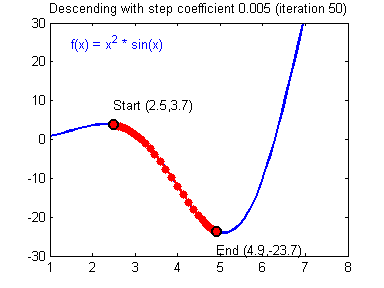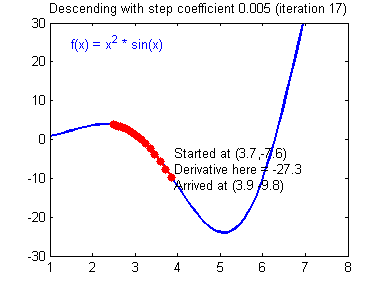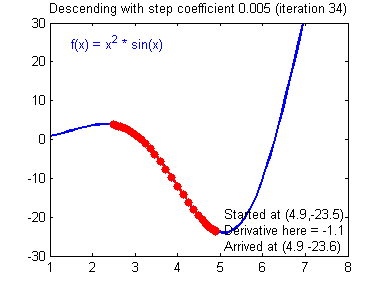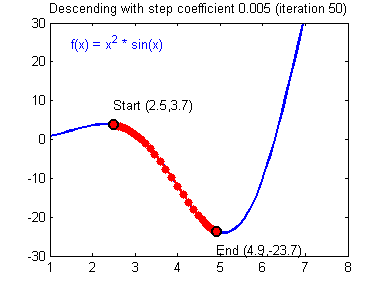差的学习率（learning rate）大小，训练开始不久，就在最小值附近跳动，难以收敛：
# planar数据集生成
import numpy as np
def load_planar_dataset():
np.random.seed(1)
m = 400 # number of examples
N = int(m/2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m,D), dtype='float32') # data matrix where each row is a single example
Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2):
ix = range(N*j,N*(j+1))
t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
import tensorflow as tf
# 加载数据
X, Y = load_planar_dataset()
# 定义神经网络结构
n_x, n_h, n_y = X.shape[0], 4, Y.shape[0]
m = X.shape[1]
# 参数初始化
W1 = tf.Variable(tf.random_normal([n_h, n_x], stddev=1, seed=1))
b1 = tf.Variable(tf.zeros([n_h, 1]))
W2 = tf.Variable(tf.random_normal([n_y, n_h], stddev=1, seed=1))
b2 = tf.Variable(tf.zeros([n_y, 1]))
# 数据输入
x = tf.placeholder(tf.float32, shape=(n_x, None), name='x-input')
y_ = tf.placeholder(tf.float32, shape=(n_y, None), name='y-input')
# 前向传播
z1 = tf.matmul(W1, x) + b1
a1 = tf.nn.tanh(z1)
z2 = tf.matmul(W2, a1) + b2
a2 = tf.nn.sigmoid(z2)
# 成本函数 & 训练图
cost = - tf.reduce_sum(tf.add(tf.multiply(y_ , tf.log(a2)), tf.multiply(1-y_ ,tf.log(1-a2)))) / m
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(cost) # 0.1 为 learning_rate
# train_step = tf.train.AdamOptimizer(0.001).minimize(cost)
# 创建 Session，运行
with tf.Session() as sess:
# 全局参数初始化
init_op = tf.global_variables_initializer()
sess.run(init_op)
# 训练模型
num_iterations = 10000
for i in range(num_iterations):
sess.run(train_step, feed_dict={x: X, y_: Y})
if i % 1000 == 0:
total_cost = sess.run(cost, feed_dict={x: X, y_: Y})
print ("Cost after iteration %i: %f" %(i, total_cost))
# 启用TensorBoard
import os
if not os.path.exists('log'):
os.mkdir('log')
logdir = os.path.join(os.getcwd(), 'log') # 将日志写到当前工作目录下的log文件夹
print('请复制以下代码到cmd，执行，启动tensorboard：\n', 'tensorboard --logdir=' + logdir)
writer = tf.summary.FileWriter(logdir, tf.get_default_graph())
writer.close()